Hello, my name is Anna Hansen. I just finished my sophomore year at UW - Stout and I am very excited to be starting research this summer with the other Lakes Reu students and faculty. I am pursuing a degree in Applied Mathematics and Computer Science with a concentration in Business Management. I also have two minors, one in Spanish as well as one in Project Management. I am originally from Eau Claire, WI, and originally chose to go to Stout for Math Education and to play volleyball. In my free time, I like to be outside, play volleyball and spend time with friends and family. I was very interested in this opportunity as I will be using my math skills to find what amount of water is needed to grow the greatest yield of kidney beans as well as seeing how Chippewa Valley Bean operates from a business standpoint.

Over the past two weeks, our team has been looking at articles to see what past researchers have done to solve similar problems. An article that we found very interesting is Tragedy of the Commons in Plant Water Use written by Zea-Cabrera et al. in 2006. In this article, they talk about the relationship between plant biomass and soil moisture. Soil Moisture and Plant Biomass are both modeled by these differential equations.

We want to begin by looking at the differential equation for soil moisture. It is important to look at this equation first because you need the soil moisture to create biomass. 𝑑𝑆𝑑𝑡 signifies the change in soil moisture over the change in time, 𝑆= Soil moisture, 𝑡= time. We then look into the equation and see 𝐼= Rainfall 𝐾𝑠𝑆𝑐= Soil drainage 𝐵(𝛾[𝑠−𝑠𝑤]𝑘+[𝑠−𝑠𝑤])= Root uptake. These three factors, factor into the change in soil moisture over time. By looking at this equation, we can see that the soil moisture will be what is left from the rain fall, after some has seeped through the soil and some water has been taken into the roots by the plant. This will leave us with a number that is the remaining soil moisture in the ground.
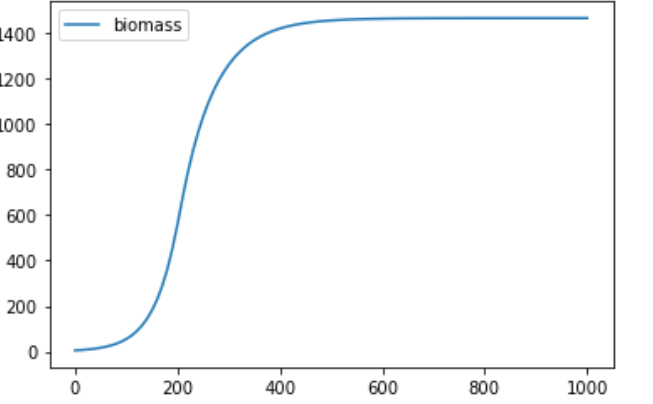
The second differential equation talks about the change in biomass over the change in time 𝑑𝐵𝑑𝑡 where 𝐵= Biomass and 𝑡= time. In this equation we see that there are two terms inside of the whole biomass term, these two terms are (𝛼[𝑠−𝑠𝑤]𝑘+[𝑠−𝑠𝑤])= Energy Production, and 𝛽 = Energy for Maintenance. By looking at this equation you can see how the plant is either growing or dying. If energy production is greater than the energy for maintenance, then the plant is growing. If the energy for maintenance is greater than the energy production, then the plant is dying because it is not able to maintain itself.
To analyze these equations, we looked at equilibrium solutions and well as graphed these two differential equations using python. In python we coded the two differential equations so we could visually see what they looked like. By using python, we can manipulate the variables to see what changes can be made to affect the graph.
In the upcoming weeks, we hope to find more equations from articles that are similar to these. We are also going to be trying to build new equations from these equations to help create an equation that will model how much water is needed to get the maximum kidney bean yield. We believe that the soil moisture and biomass equations will be helpful in the future as we are studying how water affects the total yield of kidney beans.




No comments:
Post a Comment